
|
https://theza2.blogspot.com (Cải thiện tốc độ truy cập, giao diện thân thiện hơn) Kính mời mọi người chuyển qua nhà mới ◕ Lời nhắn: ⊱ Mình học Bách Khoa nên ai đó ghét Bách Khoa thì có thể lặng lẽ đi ra ⊱ Mình là dân Thanh Hóa nên ai đó ghét Thanh Hóa cũng có thể lặng lẽ rời đi ⊱ Mình học cơ khí, trang này chỉ làm ra theo sở thích nên nếu thấy không hài lòng có thể nhẹ nhàng tắt trang ⊱ Mình hiện tại có những việc riêng phải bận cho cuộc sống của mình, sẽ không còn thường xuyên hồi đáp các bình luận, mong được lượng thứ.. | |
|---|---|
 | ◕ Dịch vụ: Nhận thiết kế Form mẫu Excel, Google Sheet: ⊱ Hỗ trợ quản lý, chiết xuất dữ liệu; Tạo bảng báo cáo, thống kê nhanh; ⊱ Tạo hệ thống thiết lập và quản lý tiến độ công việc một cách trực quan; Tạo bảng nhập liệu, tính toán hỗ trợ công việc.. ◕ Dùng thử: Chương trình phần mềm xếp thép tối ưu ⊱ Đây là chương trình mình viết ra để hỗ trợ công việc tính toán đầu vào vật tư thép hình dạng thanh (L, H, U, ...) (Nhắn tin trực tiếp tới fanpage Theza2 để trao đổi) |
| ☆ Công cụ tính tọa độ Gauss 1:25000 |
| • Số hiệu → Tọa độ • |
| • Tọa độ → Số hiệu • |
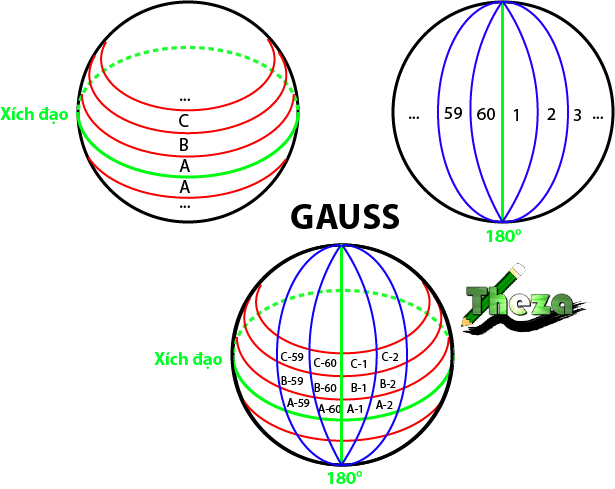

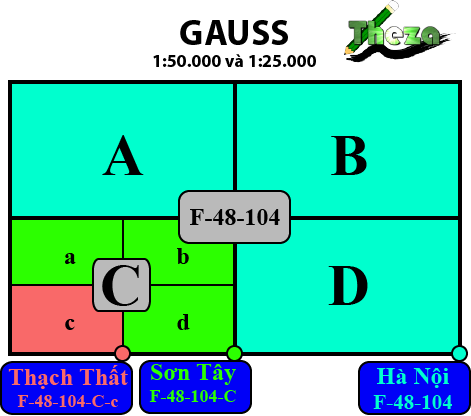
| ✡ Số hiệu → Tọa độ |
| _Giả sử M có số hiệu là P-Q-X₁-X₂-X₃
_Vĩ độ: +Bán cầu bắc: $$4(P - 1) + \frac{{11 - {\mathop{\rm int}} [({X_1} - 1)/12]}}{3} + \frac{{1 - {\mathop{\rm int}} [({X_2} - 1)/2]}}{6} + \frac{{1 - {\mathop{\rm int}} [({X_3} - 1)/2]}}{{12}}$$ +Bán cầu nam: $$4P - \frac{{11 - {\mathop{\rm int}} [({X_1} - 1)/12]}}{3} - \frac{{1 - {\mathop{\rm int}} [({X_2} - 1)/2]}}{6} - \frac{{1 - {\mathop{\rm int}} [({X_3} - 1)/2]}}{{12}}$$ _Kinh độ (kết quả dương là độ kinh Tây, âm là độ kinh Đông):$$180 - 6{Q} + \frac{{11 - \bmod [({X_1} - 1)/12]}}{2} + \frac{{1 - \bmod [({X_2} - 1)/2]}}{4} + \frac{{1 - \bmod [({X_3} - 1)/2]}}{8}$$ |
|---|
| Ví dụ: F-30-35-C-b
_Khi đó:P=F=6; Q=30; X₁=35; X₂=C=3; X₃=b=2 _Vĩ độ:$$\matrix{ 4.(6 - 1) + \frac{{11 - {\mathop{\rm int}} [(35 - 1)/12]}}{3} + \frac{{1 - {\mathop{\rm int}} [(3 - 1)/2]}}{6} + \frac{{1 - {\mathop{\rm int}} [(2 - 1)/2]}}{{12}}\\ = 4.5 + \frac{{11 - 2}}{3} + \frac{{1 - 1}}{6} + \frac{{1 - 0}}{{12}}\\ = 23^\circ 5'00'' }$$ (23°5'00'' vĩ độ Bắc) _Kinh độ:$$\matrix{ 180 - 6.30 + \frac{{11 - \bmod [(35 - 1)/12]}}{2} + \frac{{1 - \bmod [(3 - 1)/2]}}{4} + \frac{{1 - \bmod [(2 - 1)/2]}}{8}\\ = 180 - 6.30 + \frac{{11 - 10}}{2} + \frac{{1 - 0}}{4} + \frac{{1 - 1}}{8}\\ = 0^\circ 45'00'' }$$ (0°45'00'' kinh độ Tây) |
| ✡ Tọa độ → Số hiệu |
| _Giả sử M có tọa độ: m độ x ; n độ y
(m,n là tọa độ ; x là Bắc hoặc Nam ; y là Đông hoặc Tây) Ta tìm P-Q-X1-X2-X3 _Tính P: P= int(m/4 +1) $$\begin{array}{l} Khi\,đó:{X_{vt}} = \,\left[ {\begin{array}{*{20}{c}} {Bac:}&{3.[m - 4(P - 1){\rm{]}}}\\ {Nam:}&{3.(4P - m)} \end{array}} \right.\,\\ \Rightarrow {X_{vt}} = {\rm{\{ }}11 - {\mathop{\rm int}} {\rm{[}}({X_1} - 1)/12{\rm{]\} + }}\frac{{{\rm{\{ }}1 - {\mathop{\rm int}} {\rm{[}}({X_1} - 1)/2{\rm{]\} }}}}{2}{\rm{ + }}\frac{{{\rm{\{ }}1 - {\mathop{\rm int}} {\rm{[}}({X_1} - 1)/2{\rm{]\} }}}}{4}\,\,(1) \end{array}$$ _Tính Q: +Tây: Q= int(31 - n/6) +Đông: Q= int(31 + n/6) $$\begin{array}{l} Khi\,đó:{X_{kt}} = \,\left[ {\begin{array}{*{20}{c}} {Tay:}&{2.{\rm{[n - }}180 + 6Q{\rm{]}}}\\ {Dong:}&{2.{\rm{[ - n - }}180 + 6Q{\rm{]}}} \end{array}} \right.\,\\ \Rightarrow {X_{kt}} = {\rm{\{ }}11 - \bmod {\rm{[}}({X_1} - 1)/12{\rm{]\} + }}\frac{{{\rm{\{ }}1 - \bmod {\rm{[}}({X_1} - 1)/2{\rm{]\} }}}}{2}{\rm{ + }}\frac{{{\rm{\{ }}1 - \bmod {\rm{[}}({X_1} - 1)/2{\rm{]\} }}}}{4}\,\,(2) \end{array}$$ _Tính X1-X2-X3: giải hệ (1),(2) |
| Ví dụ: 50°5'0" Bắc , 97°37'30" Tây
(Khi đã hiểu rồi thì mọi người chỉ cần bấm máy tính tầm 1 phút là tìm được đáp án thôi) Ta tìm P-Q-X1-X2-X3 _Tính P: P= int(50°5'0"/4 +1)=13 $$\begin{array}{l} Khi\,đó:{X_{vt}} = \,3.[m - 4(P - 1){\rm{]}}\, = 3.[{50^ \circ }5'0'' - 4(13 - 1){\rm{]}}\, = 6,25 = 6 + \frac{0}{2} + \frac{1}{4}\\ \Rightarrow 6 + \frac{0}{2} + \frac{1}{4} = {\rm{\{ }}11 - {\mathop{\rm int}} {\rm{[}}({X_1} - 1)/12{\rm{]\} + }}\frac{{{\rm{\{ }}1 - {\mathop{\rm int}} {\rm{[}}({X_2} - 1)/2{\rm{]\} }}}}{2}{\rm{ + }}\frac{{{\rm{\{ }}1 - {\mathop{\rm int}} {\rm{[}}({X_3} - 1)/2{\rm{]\} }}}}{4}\,\,\\ \Rightarrow \left\{ \begin{array}{l} 6 = 11 - {\mathop{\rm int}} {\rm{[}}({X_1} - 1)/12{\rm{]}}\\ 0 = 1 - {\mathop{\rm int}} {\rm{[}}({X_2} - 1)/2{\rm{]}}\\ 1 = 1 - {\mathop{\rm int}} {\rm{[}}({X_3} - 1)/2{\rm{]}} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} 5 = {\mathop{\rm int}} {\rm{[}}({X_1} - 1)/12{\rm{]}}\\ 1 = {\mathop{\rm int}} {\rm{[}}({X_2} - 1)/2{\rm{]}}\\ 0 = {\mathop{\rm int}} {\rm{[}}({X_3} - 1)/2{\rm{]}} \end{array} \right.\,\,(1) \end{array}$$ _Tính Q: Q= int(31 - n/6)=int(31 - 97°37'30"/6)=14 $$\begin{array}{l} Khi\,đó:{X_{kt}} = 2.{\rm{[n - }}180 + 6Q{\rm{]}} = 2.{\rm{[9}}{{\rm{7}}^ \circ }{\rm{37'30'' - }}180 + 6.14{\rm{]}} = 3,25 = 3 + \frac{0}{2} + \frac{1}{4}\\ \Rightarrow 3 + \frac{0}{2} + \frac{1}{4} = {\rm{\{ }}11 - \bmod {\rm{[}}({X_1} - 1)/12{\rm{]\} + }}\frac{{{\rm{\{ }}1 - \bmod {\rm{[}}({X_2} - 1)/2{\rm{]\} }}}}{2}{\rm{ + }}\frac{{{\rm{\{ }}1 - \bmod {\rm{[}}({X_2} - 1)/2{\rm{]\} }}}}{4}\,\,(2)\\ \Rightarrow \left\{ \begin{array}{l} 3 = 11 - \bmod {\rm{[}}({X_1} - 1)/12{\rm{]}}\\ 0 = 1 - \bmod {\rm{[}}({X_2} - 1)/2{\rm{]}}\\ 1 = 1 - \bmod {\rm{[}}({X_3} - 1)/2{\rm{]}} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} 8 = \bmod {\rm{[}}({X_1} - 1)/12{\rm{]}}\\ 1 = \bmod {\rm{[}}({X_2} - 1)/2{\rm{]}}\\ 0 = \bmod {\rm{[}}({X_3} - 1)/2{\rm{]}} \end{array} \right.\,\,(2) \end{array}$$ _Tính X1-X2-X3: Từ (1),(2) ta có: $$\left\{ \begin{array}{l} \left\{ \begin{array}{l} 5 = {\mathop{\rm int}} {\rm{[}}({X_1} - 1)/12{\rm{]}}\\ 8 = \bmod {\rm{[}}({X_1} - 1)/12{\rm{]}} \end{array} \right. \Rightarrow {X_1} - 1 = 5.12 + 8 = 68 \Leftrightarrow {X_1} = 69\\ \left\{ \begin{array}{l} 1 = {\mathop{\rm int}} {\rm{[}}({X_2} - 1)/2{\rm{]}}\\ 1 = \bmod {\rm{[}}({X_2} - 1)/2{\rm{]}} \end{array} \right. \Rightarrow {X_2} - 1 = 1.2 + 1 = 3 \Leftrightarrow {X_2} = 4\\ \left\{ \begin{array}{l} 0 = {\mathop{\rm int}} {\rm{[}}({X_3} - 1)/2{\rm{]}}\\ 0 = \bmod {\rm{[}}({X_3} - 1)/2{\rm{]}} \end{array} \right. \Rightarrow {X_3} - 1 = 0.2 + 0 = 0 \Leftrightarrow {X_3} = 1 \end{array} \right.$$ Vậy P-Q-X1-X2-X3 là 13-14-69-4-1 = N-14-69-D-a |